Building on earlier empirical and simulation-based work, this month focused on defining the mathematical model that describes how internal leg movements can influence the robot's global orientation in microgravity. The system was modelled as a non-holonomic free-floating body, with no external torque or fixed base. As in the classic falling cat problem, reorientation must emerge entirely from internal actuation - specifically, coordinated changes in the robot's limb configuration. The body was described with 6 DoF, but control efforts focused on roll (ϕ) and pitch (θ). Each leg has 2 DoF (extension and swing), giving 8 independent inputs. Using this, the control problem was defined as an underdetermined linear system, where the Jacobian:
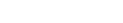
maps joint velocities to changes in roll and pitch rates:
To solve for desired joint velocities given a roll/pitch error vector, I used the Moore–Penrose pseudoinverse:


Where e = [ϕ,θ]^⊤ is the current angular error and KK is a proportional gain matrix. This formulation ensured the selected joint velocities were optimal (minimum-norm) for reducing the attitude deviation at each timestep. A key requirement for this to work in simulation was having access to a real-time estimate of the system’s moment of inertia, which changes as the legs extend or swing. To support this, I had previously trained a degree-2 polynomial regression model that predicts the centre of mass (CoM) displacement from the nominal body origin based on 8 inputs: one for each leg’s swing and extension value. These predictions fed directly into updated inertia matrix calculations via the Huygens-Steiner theorem. Testing this controller in PyBullet with gravity disabled, I observed measurable improvements in rotational convergence. Unlike earlier bandit-only strategies, which operated via action selection, this Jacobian-based controller offered continuous feedback control, enabling smooth and rapid corrections. That said, the PyBullet limitations persisted. Discontinuities during foot-ground contact and residual angular velocities after stopping leg motion remained a problem due to the physics engine’s limited momentum conservation. Work is ongoing to integrate this controller into the full simulation loop, with adaptive gain tuning and compatibility with the broader QuectoFSM infrastructure.
